Many phenomena and signals have structure on multiple scales. Consider how the human visual system works in recognizing objects: we see objects on larger scales (like human faces or trees), but then we also recognize objects at smaller scales (eyes or leaves). While our brains are able to extract information from multiple scales very efficiently, how do we teach a computer to do the same?
Our early work centered on pyramidal decompositions, which is a predecessor to scale-space representations. Conventionally, linear filters have been used in pyramidal decomposition techniques. In order to circumvent various drawbacks of linear filters and wavelet-based methods, such as ringing artifacts and the Gibbs phenomenon, nonlinear pyramidal transforms have shown to be efficient tools in heavy-tailed noise environments as well as in situations in which images contain sharp transitions and impulsive information. In [1-6], we proposed the so-called block-median pyramidal transform, which allows for perfect signal reconstruction. The block structure allows us to analytically compute probability density functions of the transform coefficients by relying on results from statistical analysis of stack filters. This makes it possible to apply these pyramidal transforms for denoising applications using analytical methods, as opposed to heuristics.
In [7], we proposed to model the structure of the transform coefficients as a Markov random field (MRF), which includes both within-scale and between-scale interactions (using an Ising model). The likeliest random field realization for the entire scale-space transform representation is obtained by Gibbs sampling. The main advantage of this method is that we are explicitly representing the interactions between transform coefficients not only spatially, but across scales, capturing the multiscale nature of the signal.
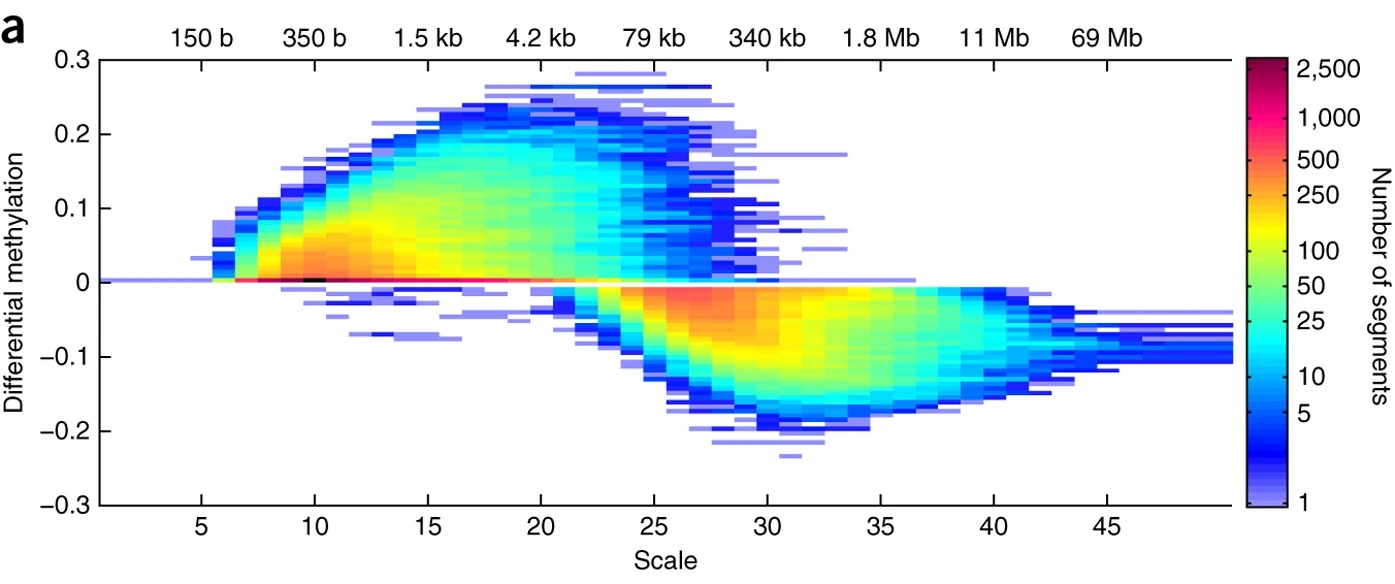
We have also explored the multiscale nature of genomic signals using Gaussian scale-space representations in [8]. For example, the figure on the right shows significant hypermethylation on the small scales and significant hypomethylation on the large genomic length scales. Such methods make it apparent that genomic information exists on multiple genomic length scales simultaneously, ranging from bases to megabases.
In the case of cancer, somatic mutations are also not uniformly distributed within genes, but are found in clusters of different genomic length scales [9].
Publications
- V. Melnik, I. Shmulevich, K. Egiazarian, J. Astola, “Iterative Block-Median Pyramid Transform-Based Denoising,” Proceedings of SPIE Wavelet Applications in Signal and Image Processing VII, Denver, CO, July 18-23, 1999.
- V. Melnik, I. Shmulevich, K. Egiazarian, J. Astola, “Image Denoising Using a Block-Median Pyramid,” IEEE International Conference on Image Processing, Kobe, Japan, October 25-28, 1999.
- V. Melnik, K. Egiazarian, I. Shmulevich, P. Kuosmanen, “A Tree Of Median Pyramidal Decomposions With An Application To Signal Denoising,” IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, June 5-9, 2000.
- I. Shmulevich, V. Melnik, K. Egiazarian, “Combination of transform based denoising and stack filtering for non-Gaussian noise suppression,” Proceedings of IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Antalya, Turkey, June 20-23, 1999.
- V. Melnik, I. Shmulevich, K. Egiazarian, and J. Astola, “Block-Median Pyramidal Transform: Analysis and Denoising Applications,” IEEE Transactions on Signal Processing, Vol. 49, No. 2, pp. 364-372, February 2001.
- V. Melnik, I. Shmulevich, K. Egiazarian, J. Astola, “Image Denoising Based on Locally-Adaptive Filtering in The Median Pyramidal Transform Domain,” IEEE – EURASIP Workshop on Nonlinear Signal and Image Processing (NSIP-01), Baltimore, Maryland, June 3-6, 2001.
- I. Gluhovsky, V. Melnik, I. Shmulevich, “Markov Random Field Modeling in Median Pyramidal Transform Domain for Denoising Applications,” Journal of Mathematical Imaging and Vision, Vol. 16, pp. 237-249, 2002.
- T. A. Knijnenburg, S. A. Ramsey, B. P. Berman, K. A. Kennedy, A.F.A. Smit, L. F.A. Wessels, P. W. Laird, A. Aderem, I. Shmulevich, “Multiscale representation of genomic signals,” Nature Methods, Vol. 11, pp. 689–694, 2014.
- W. Poole, K. Leinonen, I. Shmulevich, T. Knijnenburg, B. Bernard, “Multiscale mutation clustering algorithm identifies pan-cancer mutational clusters associated with pathway-level changes in gene expression,” PLoS Computational Biology, Vol. 13, No. 2, e1005347, 2017.


 shmulevich.isbscience.org/research/multiscale-methods/
shmulevich.isbscience.org/research/multiscale-methods/