The class of monotone Boolean functions (MBFs) is one of the most widely used and intensely studied classes of Boolean functions. Attention has been focused on it in such diverse fields as game theory, computational learning theory, harmonic analysis, and signal processing. In the latter, they have mainly been used for the design and study various classes of nonlinear digital filters, such as stack filters. These filtering operations have seen wide application in image processing tasks and in other applications where the noise sources are non-Gaussian or non-additive. Developing analytical tools capable of determining which of these filters should be used in a given application is thus of great importance. 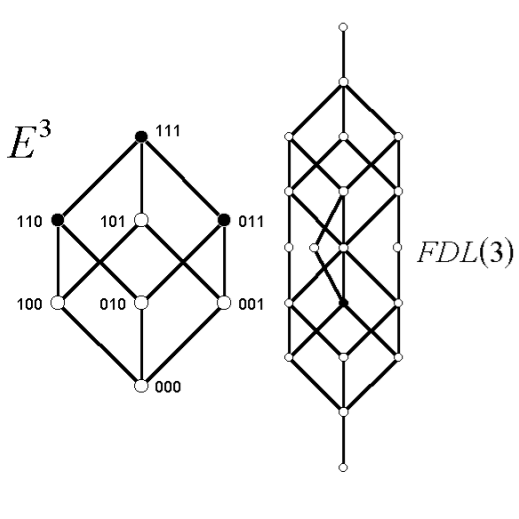
The set of all MBFs of n variables consists of all closed from above subsets of En, the n-dimensional hypercube. The set of these functions is also partially ordered by the same relation as En and is called the Free Distributive Lattice on n generators, denoted by FDL(n). The figure on the right shows an example of the function f = x1x2 + x2x3 on the 3-cube and its location in FDL(3), painted with black circles. FDL(n) is also known as Dedekind’s number and is only known for n ≤ 8. Using a statistical approach in [1], we derived an asymptotic formula for FDL(n) and posed a conjecture that the distribution of functions relative to the number of minimal true vectors (or equivalently, terms in the disjunctive normal form) is asymptotically Normal, if all monotone Boolean functions are equiprobable. This conjecture was proved in [2]. Further characterization of so-called special monotone Boolean functions was described in [3] and applied to statistical analysis of stack filters and Lyapunov exponents of monotone Boolean networks [8].
Our work also focused on the development of theories of certain classes of monotone Boolean functions, including idempotent, reversely symmetric, and compact monotone Boolean functions [3-7]. For example, the property of idempotence ensures that a second pass of the same filter (defined by the MBF) over the signal does not change the output beyond the first pass of the filter.
Publications
- I. Shmulevich, T.M. Sellke, M. Gabbouj, E.J. Coyle, “Stack Filters and Free Distributive Lattices,” Proceedings of the 1995 IEEE Workshop on Nonlinear Signal and Image Processing, Halkidiki, Greece, 1995, pp. 927-930.
- A. D. Korshunov, I. Shmulevich, “On the Distribution of the Number of Monotone Boolean Functions Relative to the Number of Lower Units,” Discrete Mathematics, Vol. 257, pp. 463-479, 2002.
- A. D. Korshunov, I. Shmulevich, “The Number of Special Monotone Boolean Functions and Statistical Characteristics of Stack Filters,” Discrete Analysis and Operations Research, vol. 7, no. 3, pp. 17-44, June 2000. (in Russian)
- I. Shmulevich, E.J. Coyle, “Generation of Reversely Symmetric Monotone Boolean Functions,” Proceedings of the IASTED International Conference on Signal and Image Processing, New Orleans, LA, 1997, pp. 399-402.
- I. Shmulevich, “Generation of Idempotent Monotone Boolean Functions,” Proceedings of the IX European Signal Processing Conference, Island of Rhodes, Greece, 1998, pp. 1405-1407.
- I. Shmulevich, E.J. Coyle, “Compact Monotone Boolean Functions,” Proceedings of the IASTED International Conference on Signal Processing and Communications, Gran Canaria, Canary Islands, Spain, 1998, pp. 235-237.
- I. Shmulevich, E.J. Coyle, “On the Structure of Idempotent Monotone Boolean Functions,” Proceedings of NOBLESSE Workshop on Non-Linear Model Based Image Analysis, Glasgow, Scotland, 1998, Springer-Verlag, pp. 339-344.
- I. Shmulevich, “On the Lyapunov Exponent of Monotone Boolean Networks,” Mathematics, Vol. 8, 1035, 2020.


 shmulevich.isbscience.org/research/monotone-boolean-functions/
shmulevich.isbscience.org/research/monotone-boolean-functions/